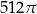/Szkoła średnia/Równania/Trygonometryczne/Stopnia 3

Zadanie nr 1020980

Oblicz sumę wszystkich rozwiązań równania

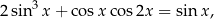
2 sin 3x + cos xco s2x = sin x,

które należą do przedziału [− 8π ,24π] .

Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy dane równanie.

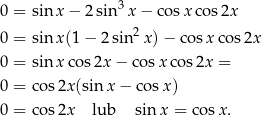
3 0 = sin x− 2sin x− cosx cos2x 0 = sin x(1− 2sin2 x)− cosx cos 2x 0 = sin xco s2x − cos xco s2x = 0 = co s2x(sin x− cosx ) 0 = co s2x lub sin x = co sx.

Po drodze skorzystaliśmy ze wzoru:

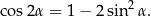
cos2α = 1− 2sin2 α.

Rozwiązaniem pierwszego równania są liczby

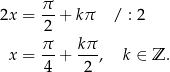
π 2x = --+ kπ / : 2 2 π- kπ- x = 4 + 2 , k ∈ Z .

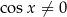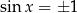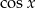Popatrzmy teraz na drugie równanie – oczywiście musi być cos x ⁄= 0 , bo inaczej sinx = ± 1 i taka wartość x nie spełnia tego równania. Możemy więc obie strony podzielić przez cosx i mamy równanie

tg x = 1.

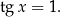
Jego rozwiązania to

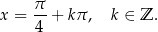
π x = --+ k π, k ∈ Z . 4

Zauważmy, że otrzymane rozwiązania równania 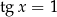tgx = 1 zawierają się we wcześniej uzyskanych rozwiązaniach równania 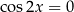co s2x = 0 . Wszystkie rozwiązania wyjściowego równania są więc postaci

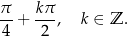
π- + kπ-, k ∈ Z . 4 2

Sprawdźmy dla jakich wartości 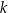k otrzymamy rozwiązania w przedziale [− 8π ,24π ] .

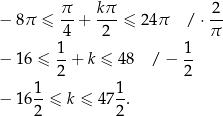
π- kπ- 2- − 8π ≤ 4 + 2 ≤ 24 π / ⋅ π 1 1 − 16 ≤ --+ k ≤ 48 / − -- 2 2 1- 1- − 16 2 ≤ k ≤ 47 2.

Interesują nas tylko całkowite wartości 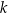k , więc 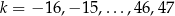k = − 16 ,−1 5,...,46,47 . Suma, która mamy obliczyć jest więc sumą 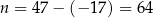n = 47− (− 17) = 64 kolejnych wyrazów ciągu arytmetycznego o różnicy 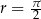r = π- 2 i pierwszym wyrazie

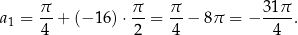
a 1 = π-+ (− 16)⋅ π-= π-− 8π = − 31π-. 4 2 4 4

Suma ta jest więc równa

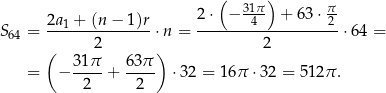
( ) 2a + (n − 1)r 2⋅ − 314π + 63 ⋅ π2 S 64 = --1------------⋅n = --------------------⋅64 = ( 2 ) 2 31π- 63π- = − 2 + 2 ⋅32 = 16π ⋅32 = 512π .

Sposób II

Przekształcamy dane równanie – tak samo jak w pierwszym sposobie skorzystamy ze wzoru

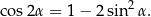
cos2α = 1− 2sin2 α.

Mamy zatem

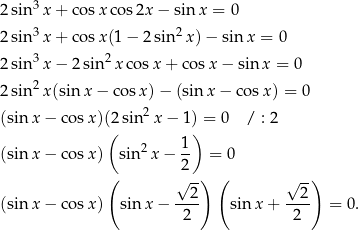
2 sin 3x + cos xco s2x − sin x = 0 3 2 2 sin x + cos x(1 − 2sin x)− sin x = 0 2 sin 3x − 2 sin 2x cosx + co sx − sinx = 0 2 sin 2x(sin x− cosx )− (sin x− cosx ) = 0 2 (sin x− cosx )(2( sin x − 1))= 0 / : 2 2 1- (sin x− cosx ) sin x − 2 = 0 ( √ --) ( √ -) --2- --2- (sin x− cosx ) sin x − 2 sinx + 2 = 0.

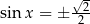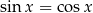Mamy zatem √2 sin x = ± -2- lub sin x = cos x . Rozwiązaniem pierwszego równania są liczby postaci

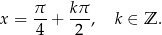
π k π x = --+ ---, k ∈ Z . 4 2

Rozwiążmy jeszcze drugie równanie – będziemy chcieli skorzystać ze wzoru

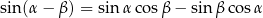
sin (α − β) = sin αco sβ − sinβ cos α

na sinus różnicy. Mamy więc

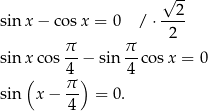
√ -- 2 sinx − co sx = 0 / ⋅---- π π 2 sinx cos --− sin --co sx = 0 ( 4 ) 4 sin x− π- = 0 . 4

Rozwiązaniem tego równania są liczby postaci

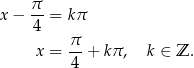
π x− --= kπ 4 x = π- + kπ , k ∈ Z . 4

Otrzymane liczby są już jednak zawarte we wcześniej otrzymanych rozwiązaniach:

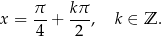
π- k-π x = 4 + 2 , k ∈ Z .

Sumę rozwiązań, które są zawarte w przedziale [− 8π,2 4π] obliczamy tak samo jak w pierwszym sposobie.  
Odpowiedź: 512 π

Wersja PDF
Rozwiązanie Losuj ponownie