/Szkoła średnia/Funkcje

Zadanie nr 6576392

Wykaż, że dla każdej liczby rzeczywistej dodatniej a prawdziwa jest nierówność

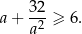
a + 32- ≥ 6. a 2
Wersja PDF

Rozwiązanie

Sposób I

Wiemy, że 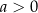a > 0 , więc daną nierówność możemy przekształcić do postaci

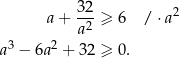
a + 32-≥ 6 / ⋅a2 a2 a3 − 6a 2 + 3 2 ≥ 0.

Aby rozłożyć wielomian z lewej strony nierówności szukamy jego pierwiastków wymiernych – sprawdzamy dzielniki wyrazu wolnego:

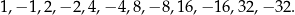
1,− 1,2,− 2,4,− 4,8,− 8,16,− 16,32 ,−3 2.

Łatwo zauważyć, że jednym z pierwiastków jest 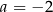a = − 2 . Dzielimy teraz ten wielomian przez (a+ 2 ) .

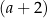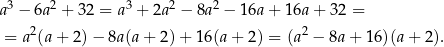
3 2 3 2 2 a − 6a + 32 = a + 2a − 8a − 1 6a+ 16a + 32 = = a 2(a+ 2 )− 8a (a+ 2 )+ 1 6(a+ 2) = (a2 − 8a+ 16)(a + 2).

Tak się przyjemnie składa, że trójmian w pierwszym nawiasie to pełen kwadrat

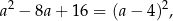
2 2 a − 8a + 16 = (a − 4) ,

więc mamy nierówność

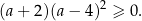
(a + 2)(a − 4)2 ≥ 0.

Nierówność ta jest spełniona dla każdej liczby dodatniej a . To oznacza, że wyjściowa nierówność też musiała być prawdziwa (bo przekształcaliśmy ją w sposób równoważny).

Sposób II

Na mocy nierówności

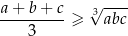
a + b + c √ ---- --------- ≥ 3 abc 3

między średnimi arytmetyczną i geometryczną liczb dodatnich mamy

∘ ---------- 32- a2-+--a2 +-32a2 3 a- a- 32- a + a2 = 3 ⋅ 3 ≥ 3 2 ⋅ 2 ⋅a2 = 3⋅ 2 = 6.
Wersja PDF
Rozwiązanie Losuj ponownie